Parametric Equation Of Circle In 3d
Parametric Equation Of Circle In 3D
What is Parametric Equation?
A parametric equation is a type of equation that expresses the coordinates of a point in terms of an independent variable or parameters. Parametric equations are used in various branches of mathematics, including calculus, linear algebra, vector calculus, and multivariable calculus. In 3D space, parametric equations can be used to describe the paths of particles, the shapes of curves, and the surfaces of objects.
Parametric Equation of Circle in 3D
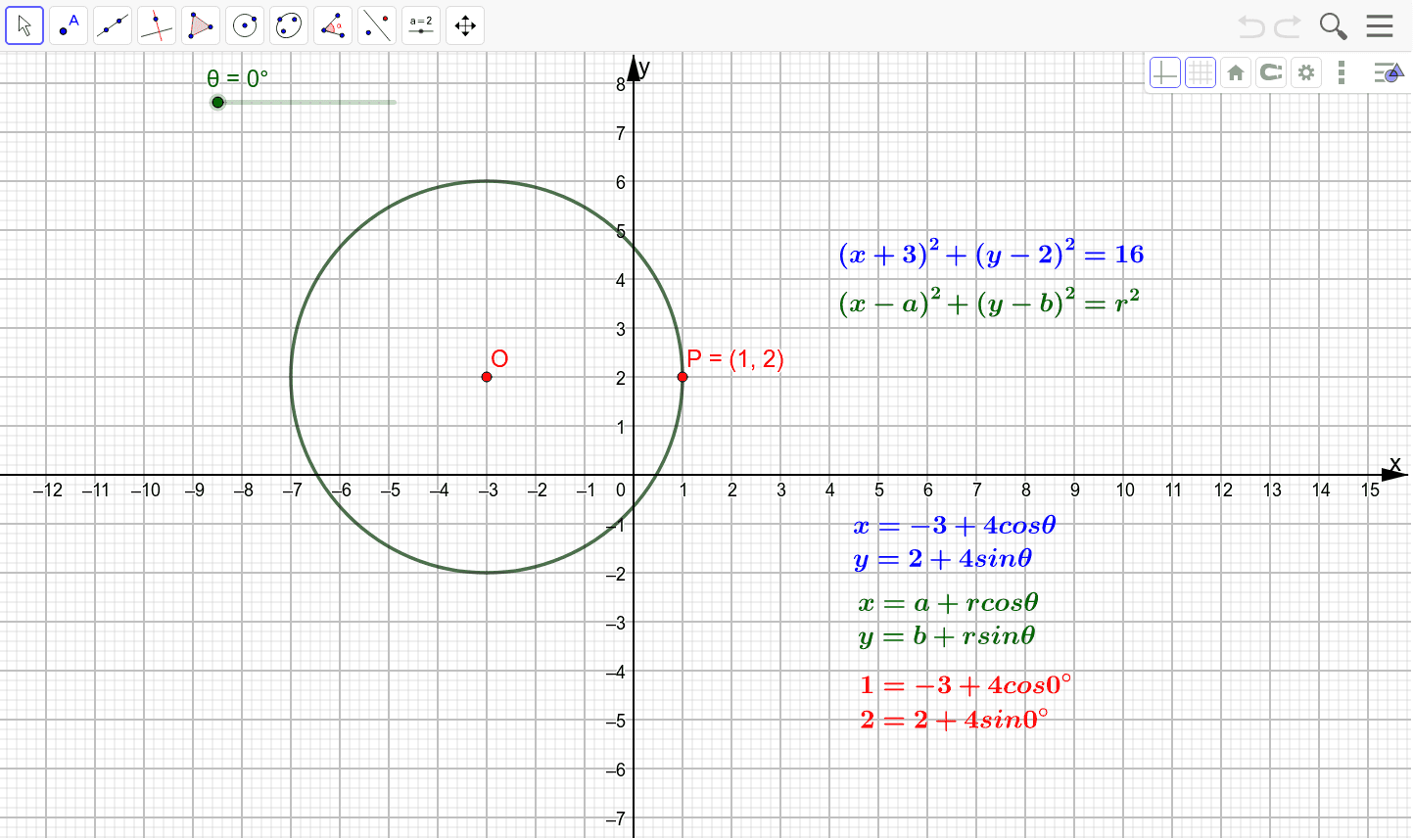
A circle in 3D space can be described by a parametric equation. The equation of a circle in 3D space can be written as follows: x = r cos(t), y = r sin(t), z = z0. Where x, y, and z are the coordinates of a point on the circle, r is the radius of the circle, t is the parameter, and z0 is the height of the circle.
Equation of a Circle in 3D:
The equation of a circle in 3D space is x = r cos (t), y = r sin (t), z = z0. The parameter t is the angle formed between the x-axis and the line joining the center of the circle and the point on the circle. The radius of the circle is denoted by r, and the height of the circle is denoted by z0.
Graphical Representation:
The graph of a circle in 3D space is a circle in the xy-plane, with the center of the circle at the origin. The radius of the circle is equal to the distance between the center of the circle and any point on the circle. The height of the circle is determined by the value of the parameter z0. The graph of a circle in 3D space is a cylinder, with the circle in the xy-plane as the base and the height determined by the parameter z0.
Example of Parametric Equation of Circle in 3D
Let us consider the following example to illustrate the concept of the parametric equation of a circle in 3D space. Consider a circle with a radius of 5 units, and a height of 2 units. The equation of this circle in 3D space is x = 5 cos (t), y = 5 sin (t), z = 2. Here, t is the parameter, x, y, and z are the coordinates of any point on the circle, r is the radius of the circle, and z0 is the height of the circle.
Conclusion
In conclusion, a parametric equation is a type of equation that expresses the coordinates of a point in terms of an independent variable or parameters. In 3D space, parametric equations can be used to describe the paths of particles, the shapes of curves, and the surfaces of objects. The equation of a circle in 3D space can be written as x = r cos (t), y = r sin (t), z = z0. Where x, y, and z are the coordinates of a point on the circle, r is the radius of the circle, t is the parameter, and z0 is the height of the circle. The graph of a circle in 3D space is a cylinder, with the circle in the xy-plane as the base and the height determined by the parameter z0.